SYSTÈMES OUVERTS (thermodynamique)

SYSTÈMES OUVERTS (thermodynamique)

SYSTÈMES OUVERTS, thermodynamique

On attribue volontiers en physique le nom de système au modèle stylisé d’un milieu naturel en vue de simplifier son étude théorique. Le solide strictement indéformable, le fluide incompressible et le gaz parfait sont des exemples classiques de tels systèmes.

En particulier, un système fermé désigne une portion invariable de matière ou, de la même façon, un ensemble donné de points matériels. Dans tous ces cas, les seuls échanges possibles avec l’environnement extérieur sont de nature énergétique. En leur absence, le système fermé est réputé isolé.

En revanche, tout échange de matière avec le milieu extérieur est le propre d’un système ouvert. Par exemple, une masse de fluide en voie de condensation représente un système fermé, mais chacune des phases considérée séparément est un système ouvert, puisque la masse de liquide croît aux dépens de la masse de vapeur.

L’utilité d’une semblable représentation s’est imposée progressivement, tant en mécanique des fluides avec l’étude des appareils à jets, des fusées et des turboréacteurs, qu’en thermodynamique, avec celle d’un grand nombre de processus physico-chimiques continus, dont notamment les mécanismes du type réaction-diffusion et le comportement de phases superficielles non autonomes. De plus, toute tentative d’interprétation de l’ordre biologique à partir des lois de la thermodynamique pose a priori un problème de système ouvert. Dans cette discipline, l’interprétation de systèmes à masses variables n’est pas récente, puisqu’elle apparaît déjà, au moins tacitement, dans l’œuvre de J. W. Gibbs sur l’équilibre des systèmes chimiques hétérogènes (Equilibrium of Non-Homogeneous Substances. Collected Works , Longmans Green, Londres, 1875-1878). Toutefois, la formulation explicite des bilans de conservation de la masse de chaque constituant, de la quantité de mouvement, de l’énergie interne ou totale (premier principe), comme celle du bilan entropique (second principe), qui régissent les différents flux d’échange entre un système ouvert et son environnement extérieur, n’intervient que beaucoup plus tard à la suite des travaux de l’école de Bruxelles, après 1930. La dénomination actuellement consacrée de système ouvert a la même origine.

Il convient de rappeler à ce sujet que, sous leur forme ordinaire, les théorèmes généraux de la mécanique comme les principes de la thermodynamique se rapportent essentiellement à des systèmes fermés. Pour en déduire la formulation appropriée aux systèmes ouverts, quelques précautions doivent être prises et quelques précisions s’imposent. Tout d’abord, la frontière de ces derniers doit être constituée d’une surface géométrique distincte en tout point de toute limite de séparation entre deux phases afin d’éviter une équivoque sur l’état de la matière qui franchit cette frontière, et l’ambiguïté qui en résulterait pour la définition même du système ouvert considéré.

C’est ainsi que dans l’exemple cité relatif à la condensation d’une vapeur, la frontière du système ouvert est située dans la phase liquide, car elle doit incorporer, en outre, la couche de transition vapeur-liquide. La phase liquide peut se présenter sous forme continue ou dispersée en brouillard. Dans ce cas, la masse M du système obéit aux égalités:

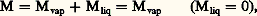et son accroissement d M a pour valeur:

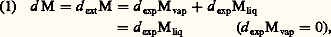où l’indice ext. désigne l’échange externe avec le milieu ambiant.

Bien entendu, la convention inverse qui revient à incorporer la couche de transition à la phase liquide, ce qui implique l’état de vapeur sur la face externe de la frontière, est pareillement acceptable, mais le choix doit être précisé dans chaque cas. Ce commentaire justifie aussi la dénomination de controled volume , adoptée parfois dans les pays anglo-saxons pour désigner un système ouvert.

L’adaptation du formalisme habituel des bilans s’obtient ensuite sans difficulté, par l’application de la règle de dérivation des intégrales de volume du type:

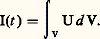Sous les réserves habituelles de continuité, cette règle s’écrit:

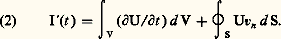Dans cette relation, U désigne une grandeur locale, fonction des coordonnées et du temps, qui peut être en particulier la masse volumique 福, l’énergie volumique 福e , la composante 福vⁱ de la quantité de mouvement ou l’entropie volumique 福s . Quant à la dérivée I (t ), elle représente l’accroissement d I/dt mesuré le long du mouvement de vitesse . Enfin, n désigne la normale extérieure à la surface frontière S.

Si cette frontière est fixe et si la vitesse v est celle de la matière, la dérivée I (t ) se rapporte à un système fermé (f ) puisque, dans ce cas, la matière est suivie dans son mouvement. L’intégrale de volume:

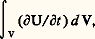au contraire, concerne l’accroissement local d’un système ouvert (o ) de volume fixe V. Dès lors, la relation (2) fournit le moyen de déduire directement l’expression des lois des systèmes ouverts, du formalisme classique relatif aux systèmes fermés, par l’opération de substitution:

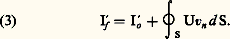Dans le cas d’une frontière comportant une section d’entrée 靖¹(vⁿ 麗 0), une section de sortie 靖(vⁿ 礪 0) et une paroi imperméable à la matière (vⁿ = 0), lorsqu’en outre la fonction U considérée, ou la grandeur massique u correspondante (U = 福u ), possède une valeur uniforme ( 福¹u ¹) répartie sur la section 靖¹ et 福²u ² répartie sur la section 靖², la substitution à introduire dans les bilans (massiques, énergétiques, enthalpiques...) des systèmes ouverts prend la forme simplifiée:

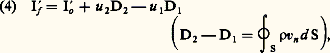où les quantités D² et D¹ désignent respectivement la valeur absolue des débits massiques de sortie et d’entrée. En particulier, l’application de l’équation (4) au bilan de masse d’un système ouvert donne, pour l’accroissement M size=1⁰ de sa masse M, la relation:

puisque le système fermé correspondant obéit à la loi de conservation M size=1^f = 0 (M du système fermé = constante). De plus, grâce à cette dernière propriété, l’application de l’équation (4) à un milieu uniforme (u ¹ = u ² = u ) conduit indifféremment à l’une des relations suivantes:

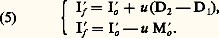Ainsi, l’expression classique du principe de la conservation de l’énergie pour un système fermé uniforme:

où d Q correspond à la forme différentielle du flux de chaleur reçu par le système envisagé, et où H représente son enthalpie, E son énergie, p sa pression et V son volume, devient pour un système ouvert: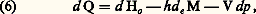

sachant que:

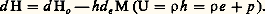Le développement de d H^o en variables: température, pression, masses, conduit à l’élimination de la constante arbitraire associée à la valeur de l’enthalpie massique h .

L’emploi de la relation (2) implique encore deux remarques. Tout d’abord, elle ne fait pas intervenir les échanges massiques effectués par diffusion avec l’environnement extérieur, mais uniquement les échanges convectifs, puisque la matière a été supposée suivie dans son mouvement. Le transport par diffusion doit donc être éventuellement incorporé au terme de surface:

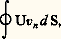de l’équation (2). Il intervient, dès lors, dans le terme d^e M du bilan de conservation de l’énergie (6).

Les équations de transport associées aux invariants de collision en mécanique statistique confirment cette obligation.

En second lieu, la validité de la relation analytique (2) n’est pas limitée au seul cas du mouvement de la matière. La vitesse considérée peut également représenter celle d’une surface mobile géométrique, comme par exemple la frontière d’un système ouvert, toujours sous les réserves habituelles de continuité. Il en résulte la possibilité d’extension de la méthode aux systèmes ouverts mobiles tels que les fusées.

À cette fin, on désigne par v^o la vitesse de l’enveloppe pour la distinguer de la vitesse v du milieu matériel. On note à ce sujet que v^o ne doit pas être définie sur toute l’étendue du volume mais seulement sur la frontière S, comme l’établit notamment la démonstration de (2) par la méthode de J. Hadamard (Cours d’analyse , de l’École polytechnique, Hermann, Paris, 1927). On écrit ensuite successivement la relation (2) pour la vitesse v de la matière (système fermé) et pour la vitesse v^o de l’enveloppe (système ouvert), ce qui entraîne par soustraction la généralisation de la loi de substitution (3) sous la forme:

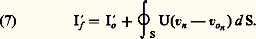Dans le cas évoqué plus haut d’une frontière comportant une section d’entrée de la matière:

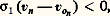une section de sortie:

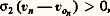et une paroi latérale imperméable:

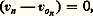la loi de substitution (7) se réduit à son tour à l’égalité (4) et la généralise.

L’étude des systèmes ouverts mobiles implique généralement le recours à un référentiel mobile et donc aux lois du mouvement relatif. Dans ce cas, la distinction s’impose entre la vitesse d’entraînement du référentiel qui correspond au mouvement d’un solide:

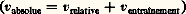et la vitesse v^o de l’enveloppe du système ouvert considéré, puisque celle-ci n’est pas nécessairement rigide.

En conclusion, la formulation correcte ainsi obtenue des bilans de masses, de quantités de mouvement, d’énergie et d’entropie des systèmes ouverts mobiles, ainsi que le caractère systèmatique de la méthode suivie, permettent, par opposition à de nombreux procédés ad hoc , un traitement direct des divers problèmes de rendements, de poussée, de travail utile ou de puissance optimale, de même qu’une appréciation des différentes pertes dans les turbo-machines, et les multiples techniques de propulsion par jets comme sont notamment les fusées.

Encyclopédie Universelle. 2012.